报告题目：Parameter estimation for the complex fractional Ornstein–Uhlenbeck processes with Hurst parameter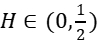

报告摘要：We study the strong consistency and asymptotic normality of a least squares estimator of the drift coefficient in complex-valued Ornstein-Uhlenbeck processes driven by fractional Brownian motion, extending  the results  of  Chen et al. (2017) to the case of Hurst parameter 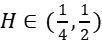and the results of  Hu et al. (2019)  to a two-dimensional case. When 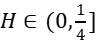,  it is found that the integrand of the estimator is not in the domain of the standard divergence operator. To facilitate the proofs, we develop a new inner product formula for functions of bounded variation in the reproducing kernel Hilbert space of fractional Brownian motion with Hurst parameter 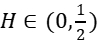. This formula is also applied to obtain the second moments of the so-called 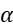-order fractional Brownian motion and the 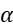-fractional bridges with the Hurst parameter .

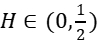报告人简介：陈勇，副教授，硕士生导师，保山学院大数据学院学术副院长。本科毕业于中国海洋大学（1998），硕士及博士毕业于北京大学（2001，2006），曾国家公派访问美国堪萨斯大学数学系。主要从事随机过程，随机分析及其应用的研究工作。在 Stoch. Process Their Appl. ，Journal of theoretical probability，Journal of Applied Probability，Journal of Statistical Planning and Inference，Journal of Mathematical Physics，Chaos, Solitons & Fractals，Kyoto Journal of Mathematics，Infin. Dimens. Anal. Quantum. Probab. Relat. Top.，ALEA Lat. Am. J. Probab. Math. Stat. 等数学和概率统计主流期刊上发表学术论文36篇。主持国家自然科学基金青年基金一项（2012-2014），地区基金两项（2019-2023，2025-2028）。

报告时间：2024年12月5日10:30-12:00

报告地点：同析4号楼322会议室